9 min to read

Batch vs. Layer vs. Instance vs. Group Normalization (+RMS, Shuffling BN) - 언제, 그리고 왜 쓰는건가요?

딥러닝에 사용되는 다양한 정규화 기법들의 심도 있는 비교 (BN vs. LN을 중심으로)

Featured image

📢 배치 정규화를 포함해 딥러닝에서 사용되는 다양한 정규화 기법들에 대한 포스팅입니다. 첫번째 페이지에서는 배치 정규화(Batch Normalization)와 층정규화(Layer Normalization)에 대해 심도 있게 비교하고, 두번째 페이지에서는 그 외의 다양한 기법에 대해 소개하겠습니다.

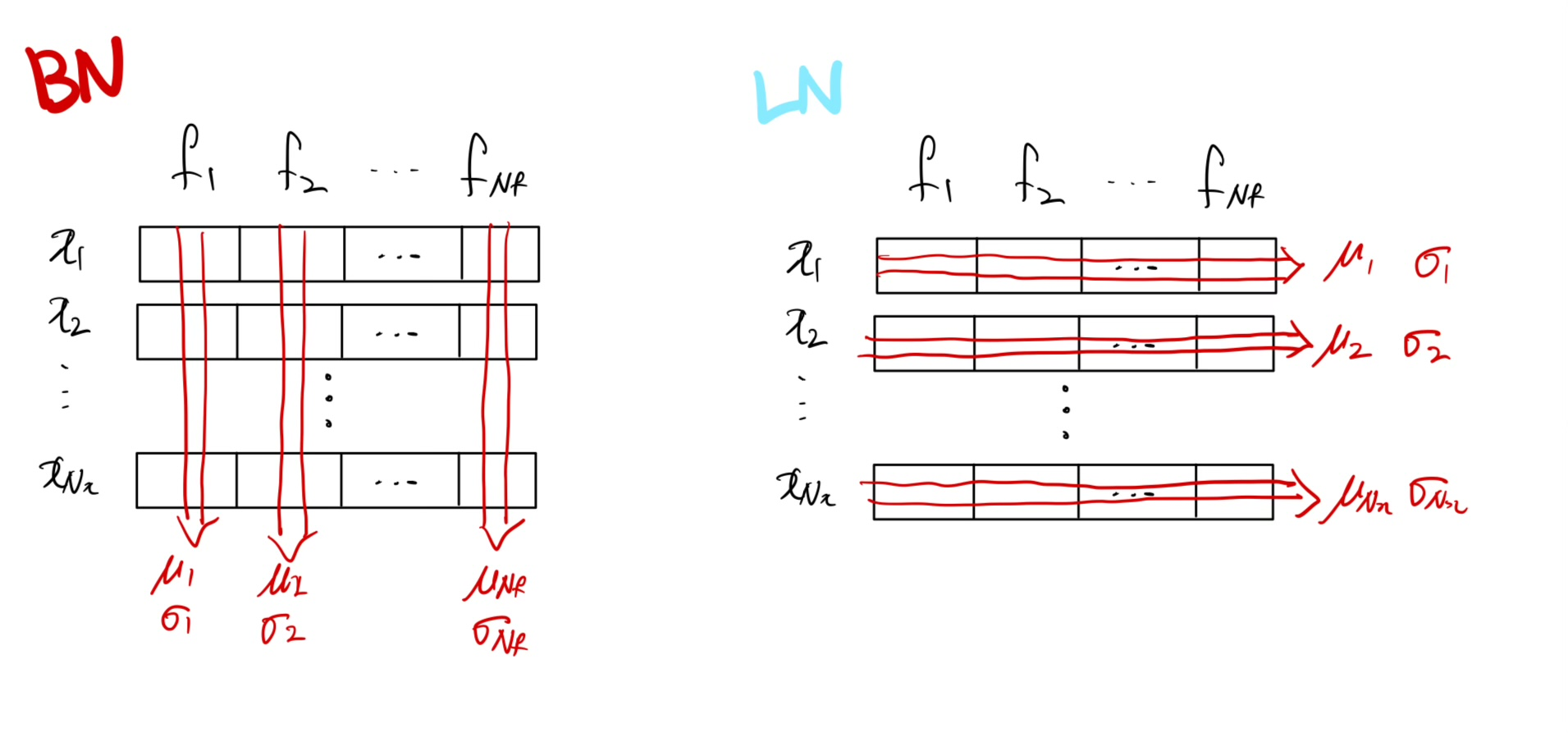
먼저 배치 정규화(batch normalization)과 층 정규화(layer normalization) 기법에 대해 알아보고 비교해보자.CNN부터 transformer까지, 항상 있는 듯 없는 듯 껴 있는 연산들이고, 코드 상에서도 딱 한줄 들어가는 존재감 없는 녀석들이다. 둘이 매번 헷갈린다. 뭔가 공변량 변화를 막아주기 위해 분포를 정규화해주는건 알겠는데…

구체적으로 어떻게 동작하는거지? 그래서 BN은 언제 쓰는거고, LN은 언제쓰는건데?

먼저 BN과 LN의 등장 배경에 있는 문제: 내부 공변량 변화(Internal covariate shift)에 대해 먼저 알아보자.

Covariate Shift & Internal Covariate Shift

공변량 변화(Covariate shift)는 학습 데이터와 테스트 데이터 사이의 분포 차이가 발생하는 현상을 의미한다. 가령 강아지로만 구성된 데이터셋으로 학습시킨 모델에게 고양이 데이터를 준다면, 강아지와 고양이 두 데이터의 (픽셀 값들의) 분포가 다르기 때문에 제대로 추론을 수행하지 못할 것이다.

이러한 covariate shift가 신경망 내부에서 일어나는 것을 내부 공변량 변화(internal covariate shift)라고 부른다. 인공 신경망은 매번 데이터가 입력될 때마다 각 층에서의 활성화 값을 출력한다. 이전 층의 활성화 값은 다음 층으로 전달된다. 문제는, 각 층을 계속할 때마다 각 층으로 입력되는 활성화 값들이 들쑥날쑥 바뀐다는 것이다. 이 문제는 층의 깊이가 깊어질 수록 더 심해진다.

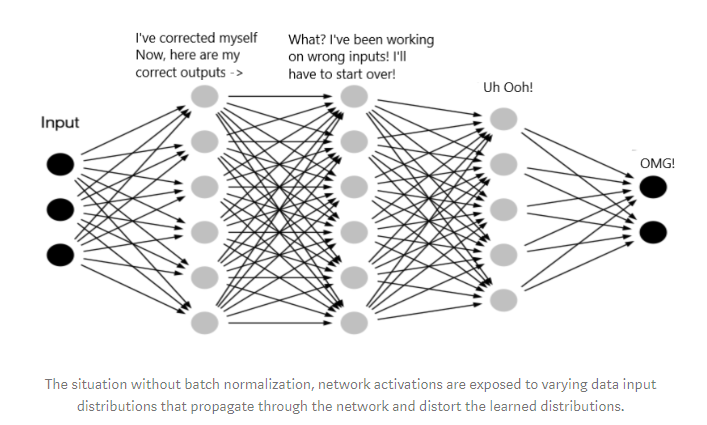
왜 그럴까? 인공 신경망에는 매 step마다 각 층의 파라미터들이 업데이트되는데, 현재 step과 다음 step의 파라미터 값들이 다르니 이 층들을 지나온 활성화 값들도 다른 값을 갖게 된다. 층의 깊이가 깊은 경우, 각 층들의 파라미터 값이 살짝만 업데이트 되어도 이러한 변화가 누적되며 뒤쪽 층에게는 상당한 변화로 다가올 것이다.

이러한 내부 공변량 변화로 인해 신경망은 계속해서 변화하는 데이터에 맞춰 학습해야 하니 학습 과정이 더 많은 step을 요구하고, 불안정한 학습을 촉발한다. 또한 gradient가 너무 작거나 큰 값으로 계속해서 누적되는 경우 gradient vanishing/exploding 문제로 이어지기도 한다.

Batch Normalization

등장한 연도 자체는 BN이 LN보다 먼저 나왔다(Ioffe et al. ICML’15). BN은 내부 공변량 변화(Internal covariate shift)라는 문제를 해결하고자 도입되었다.

배치 정규화는 미니배치 내의 활성화값들의 평균과 표준편차를 구해 standard scaling을 적용하여 활성화 값들의 분포를 표준정규분포로 만들어주어 내부 공변량 변화를 없애고 학습을 안정적이고 빨리 수렴하도록 도와준다.

연산은 다음과 같다:

  1. 현재 미니배치 안에 존재하는 활성화 값들의 평균($\mu$)과 표준편차($\sigma$)를 구한다.
    • 만약 입력이 (N, C, H, W) 차원의 이미지라면, N,H,W에 대해 평균을 내어 (C) 차원을 갖는 통계값($\mu$, $\sigma$)이 계산된다.
    • 만약 입력이 (N, C, L) 차원의 시퀀스라면, N,L에 대해 평균 내어 (C) 차원 통계값이 계산된다. \(\mu=\frac{1}{N}\sum_i^Nx_i,\quad\sigma=\sqrt{\frac{1}{N}\sum_i^N(x_i-\mu)^2}\)

이 때 $N$은 배치 사이즈, $x_i$는 미니배치 내의 $i$번째 샘플의 활성화 값이다. $x_i,\mu,\sigma\in\mathbb{R}^1$이다.

  1. 각 활성화 값들을 평균으로 빼고 표준편차로 나누어 정규화한다 (Z-score/standard scaling).
\[\hat{x}_i=\frac{x_i-\mu}{\sigma+\epsilon}\]

이 때 $\epsilon$은 분모를 0으로 만들지 않기 위한 작은 상수다.

  1. 학습 가능한 scale and shift 파라미터(각각 $\gamma, \beta$)를 곱하고 더해준다. 이렇게 하는 이유는, 활성화 값의 분포를 모두 일정한 정규분포로 만들어 버리면 내부 공변량 변화는 없어진다 해도 오히려 모델의 표현력이 떨어지는데(모델이 다양한 분포를 학습하지 못함), 학습 가능한 파라미터로 분포를 적당히 조절해주어 모델의 표현력을 떨어뜨리지 않으면서 정규화를 수행하기 위함이다.
\[y_i=\gamma \hat{x}_i+\beta\]

Batch Normalization: Training vs. Inference

지금까지는 미니배치 단위로 학습할 때를 가정하고 이야기했지만, 만약 싱글 데이터포인트 단위로 입력되는 추론 단계에서는 BN이 어떻게 동작할까?

간단히, BN은 학습 도중 입력된 모든 미니배치에 대해 $\mu$와 $\sigma$의 이동평균을 저장해두고, 추론 시에 이렇게 저장된 $\mu$와 $\sigma$를 가져와 정규화를 수행한다.

BN의 장단점

BN의 장단점을 요약하면 다음과 같다:

BN의 장점

  1. 내부 공변량 변화를 막아 학습 시 수렴 속도가 빠르고 안정적인 학습이 가능하다.
  2. 위와 같은 이유로 깊은 층을 가진 신경망도 효과적으로 학습할 수 있다.
  3. 초기 가중치 설정값의 영향을 줄여준다 (뭘로 초기화하든 결국 뒤에서 정규화해주기 때문에).
  4. Overfitting을 방지하는 역할이 있다. (BN의 정규화 과정은 일종의 regularization 역할을 수행한다)

BN의 단점

  1. 배치 사이즈에 의존적이다. 작은 배치 사이즈에서는 통계값이 불안정해 오히려 학습을 방해할 수 있다.
  2. 순차적 데이터(sequence)에 대해 부적합하다. (다음 section에서 설명)
  3. 연산 overhead가 늘어난다. 어쨌든 새로운 연산 과정과 파라미터가 추가된 것이고, 학습중 매번 이동평균도 구해줘야 한다.

Batch Normalization for NLP

일반적으로 BN은 자연어 처리(NLP) 분야에서는 잘 쓰이지 못한다고 한다. 그 이유는 이미지 데이터와 시퀀스 데이터의 특성 차이 때문인데, 한 미니배치에 들어있는 모든 이미지는 동일한 shape(HxW)를 가지지만, 시퀀스 데이터는 그렇지 않고 각각의 시퀀스가 (padding을 제외하면) 제각각의 시퀀스 길이를 가지기 때문에 시퀀스 데이터에 적용하기엔 부적합하다고 볼 수 있다.

반면 CNN과 같은 모델이 이미지 데이터를 다루는 경우에는 적합하다.

Layer Normalization

층 정규화(LN) 역시 내부 공변량 변화에 대처하기 위한 정규화 기법으로, 시퀀스 데이터 학습에 취약한 BN의 단점을 개선하고자 등장하였다. 먼저 BN과 LN의 연산을 아래 그림과 함께 비교해보자.

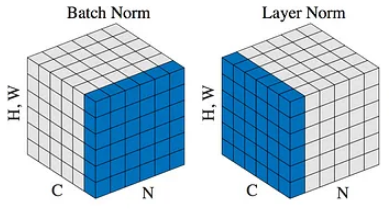
그림의 H,W는 이미지라면 height x width가 되겠지만, 시퀀스라면 시퀀스 길이로 봐도 무방하다.

LN의 연산 과정을 수식으로 나타내면 다음과 같다:

  1. 평균($\mu$)과 표준편차($\sigma$) 계산
    • 만약 입력이 (N, C, H, W) 차원인 이미지라면, C,H,W차원에 대해 평균을 내어 (N) 차원의 통계값이 계산된다.
    • 만약 입력이 (N, C, L) 차원의 시퀀스라면, N,L에 대해 평균을 낸다 (결과는 N차원).
\[\mu=\frac{1}{C}\sum_i^Cx_i,\quad\sigma=\sqrt{\frac{1}{C}\sum_i^C(x_i-\mu)^2}\]

이때, $x_i,\mu,\sigma\in\mathbb{R}^1$이다.

BN과 비교했을 때, BN에서의 배치($i=1,\dots,N$) 단위 평균/표준편차를 구하는 식이 한 데이터 포인트 내에서의 활성화값(feature; $i=1,\dots,C$)들을 평균/표준편차 내는 식으로 바뀌었다 ($C$는 임의의 임베딩 차원 혹은 채널 개수라고 하자).

  1. 정규화
\[\hat{x}_i=\frac{x_i-\mu}{\sigma+\epsilon}\]
  1. Scale and shift (BN과 동일하게 학습 가능한 파라미터 $\gamma,\beta$ 도입)
\[y_i=\gamma\hat{x}_i+\beta\]

Why Layer Normalization?

LN은 BN처럼 학습 시의 불안정성과 overfitting을 방지해주면서 배치에 대한 의존성을 줄여 자연어와 같은 시퀀스 데이터 학습을 더 효과적으로 만들어주었다.

LN의 장단점을 정리하면 다음과 같다:

LN의 장점

  1. BN의 장점과 같다 (안정적이고 빠른 수렴, overfit 방지).
  2. 배치 사이즈에 대한 의존성이 없어 시퀀스 데이터에 적용할 수 있다.
  3. BN과 다르게 학습/추론 시 동작이 같아 평균/표준편차에 대한 이동평균을 매번 계산해서 저장할 필요가 없다.

LN의 단점

  1. BN의 단점과 같이 추가적인 연산량이 도입된다(정규화, scale and shift).
  2. 각 데이터 포인트에 대해 독립적으로 연산하기 때문에 대규모 배치에서 연산 overhead가 커진다.

–page-break–

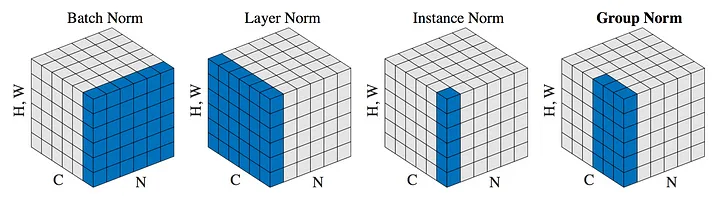
Instance Normalization, Group Normalization

Instance normalization(IN)과 group normalization(GN)은 종종 LN과 비견되곤 하는데, 그 이유는 이들 셋 모두 batch에 독립적으로 적용되기 때문이다. 미리 간단히 설명하자면, IN은 모든 채널에 대해 독립적으로(channel-wise) 평균을 계산하고, LN은 모든 채널에 대해(across) 평균을 계산한다. GN은 그 중간이라고 보면 된다.

Instance Normalization

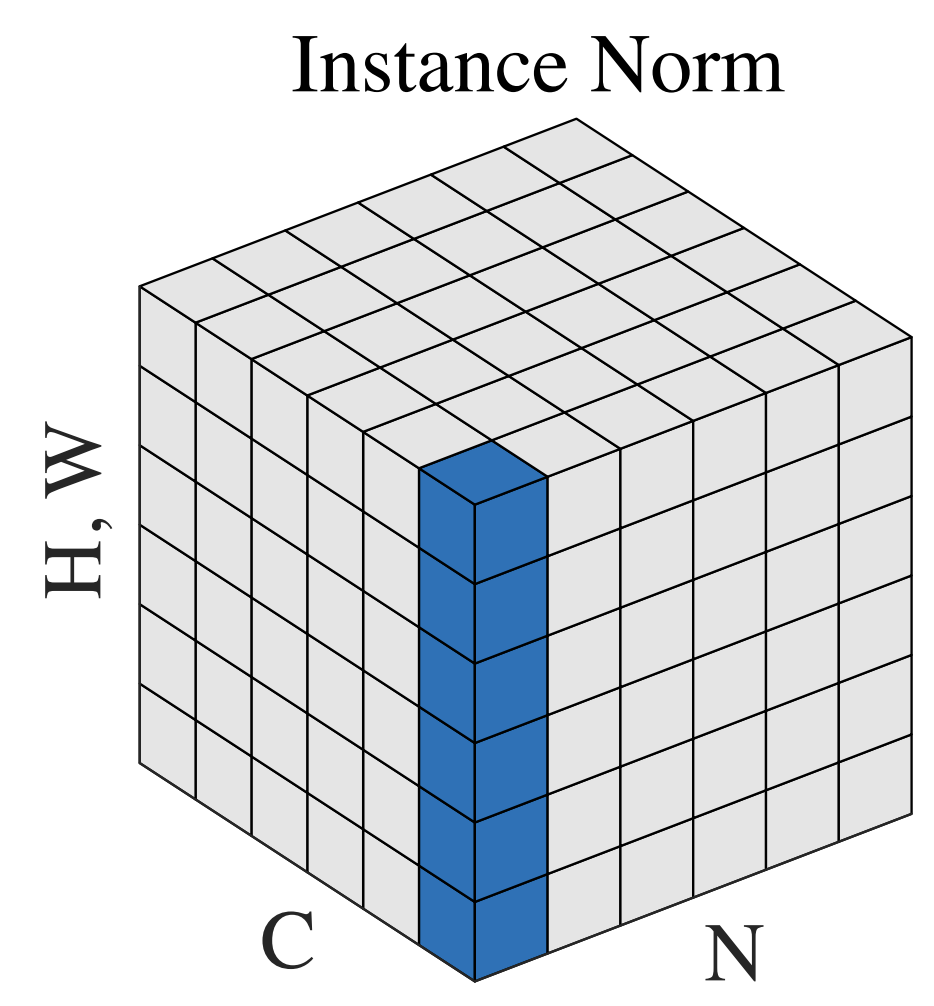
어떻게 계산되는가?

입력이 (N, C, H, W)인 이미지가 입력되었다고 가정할 때, $k$번째 채널의 평균과 표준편차(각각 $\mu,\sigma\in\mathbb{R}^{N\times C}$)의 계산식은 다음과 같다 (이때 $x_{kij},\mu,\sigma$는 스칼라):

\[\mu_k=\frac{1}{HW}\sum_i^H\sum_j^W x_{kij},\quad\sigma_k=\sqrt{\frac{1}{HW}\sum_i^H\sum_j^W(x_{kij} - \mu_k)^2}\]

Scald and shift는 BN,LN과 동일하므로 생략하겠다.

(N, C, H, W)의 이미지가 채널에 대해 독립적으로 평균이 계산돼 (즉, H, W차원에 대해 평균을 내어) (N, C) 차원의 통계값으로 변한 것을 확인할 수 있다.

만약에 (N, C, L)의 시퀀스가 입력되었다고 가정한다면(IN은 컴퓨터 비전에서 사용되기 때문에 그럴 일은 거의 없겠지만), L차원에 대해 평균내어져 (N, C) 차원의 통계값이 계산될 것이다.

언제 쓰이는가?

Style transfer 분야에서 처음 제안된 방법이다. 기존에 널리 쓰이던 BN의 경우 미니배치 내의 모든 샘플(인스턴스)에 대해 평균을 내기 때문에, 샘플들 간의 스타일 정보가 뒤섞일 위험을 가지고 있었다. 이에 따라 LN처럼 각 샘플에 대해 독립적으로 계산하는 동시에 각 BN처럼 각 채널에 대해 독립적으로 계산하는 IN이 고안되었다.

또한 논문에 따르면, 스타일 변환 작업에서는 이미지의 대비(contrast) 정보가 스타일 변환 성능을 결정짓는 중요한 특징이라고 한다. 그런데 스타일 변환을 위해 참고하는 이미지(style image)의 대비 정보가 스타일 변환의 결과로 생성된 이미지(stylized image)에도 유지되도록 모델이 학습된다고 한다. 따라서 스타일 변환의 대상이 되는 입력 이미지(content image)의 대비 정보는 오히려 학습에 방해가 되는 요소로써, IN에서는 정규화를 통해 이러한 대비 정보를 없애주는 효과가 있다고 한다.(IN은 이러한 이유로 contrast normalization이라고도 불린다).

IN은 물론 style transfer와 같은 작업에서는 효과적이나, 일반적인 분류나 object detection과 같은 작업에서는 BN에 비해 효과적이지 않을 수 있다.

Group Normalization

IN과 LN, BN을 알았다면 GN은 비교적 간단한 컨셉이다. GN은 LN, IN과 같이 배치 내의 각 샘플에 대해 독립적으로 계산하지만, IN과 달리 여러 샘플을 그룹으로 묶어 그룹 단위로 평균을 계산한다.

어떻게 계산되는가?

  1. 먼저 $C$ 채널을 $G$개의 그룹으로 나뉜다. 각 그룹은 $M=C/G$개의 그룹으로 나뉜다.
  2. 각 그룹에 대해 평균과 표준편차를 계산한다. 만약 (N, C, H, W) 차원의 이미지가 입력되었다면, $g$번째 채널 그룹에 대한 평균($\mu_g$)과 표준편차($\sigma_g$)는 다음과 같이 계산된다:
\[\mu_g=\frac{1}{MHW}\sum_g^M\sum_i^H\sum_j^Wx_{gij},\quad\sigma_g=\sqrt{\frac{1}{MHW}(x_{gij}-\mu_g)^2}\]

위 그림에서는 $G$와 $M$이 바뀌었음을 주의하라.

그룹의 크기 $M=1$인 경우 (즉, $G=C$), IN과 동일한 연산이 된다. 반대로 $M=C$인 경우 (즉, $G=1$), LN과 동일한 연산이 된다.

(N, C, H, W)의 이미지가 채널을 그룹으로 묶은 뒤 각 그룹에서 H,W에 대해 평균이 계산돼 (N, G) 차원의 통계값으로 변한 것을 확인할 수 있다.

만약에 (N, C, L)의 시퀀스가 입력되었다고 가정한다면(그럴 일은 거의 없겠지만), L차원에 대해 평균내어져 (N, G) 차원의 통계값이 계산될 것이다.

언제 쓰이는가?

GN과 IN은 아이러니하게도 LN과 그 연산이 종종 비교되곤 하지만, 사실 컴퓨터 비전 태스크에서 BN을 대체하기 위해 제안된 방법들이다 (BN은 2015년, LN과 IN은 2016년, GN은 2018년에 제안되었다). Large vision 모델들의 경우 메모리 용량의 한계로 인해 크기의 미니배치를 사용해야 하는 경우가 종종 있는데, BN의 경우 작은 배치 사이즈에서 성능이 하락하는 문제가 있었다. GN은 이에 대해 대처하기 위해 제안되었다.

GN은 배치 사이즈와 무관하게 연산되기 때문에 배치 사이즈가 작거나 가변적인 경우에서도 잘 동작하며, 이미지 분류, object detection, segmentation 등의 비전 태스크에서 BN의 대체재로 좋은 성능을 보였다.

Why Grouping?

RMS(Root Mean Square) Normalization

다시 자연어처리로 돌아오자. RMSNorm은 최근 Llama 모델에 탑재되며 NLP에서 LN의 대체재로 각광받는 방법이며(Zhang et al., ‘19), LN의 연산 비용을 줄이고자 제안되었다.

먼저 계산 과정을 보자.

  1. 만약 (N, C, L) 크기의 시퀀스 $x={x_1,\dots,x_L}$가 입력되었다고 할때, 입력 데이터 포인트에 대해 RMS(평균제곱근; L2 norm)을 계산한다.
\[RMS(x)=\sqrt{\frac{1}{L}\sum_i^Lx_i}\in\mathbb{R}^L\]
  1. 시퀀스를 1에서 구한 RMS로 나눠준다 ($\epsilon$은 작은 상수).
\[\hat{x}_i=\frac{x_i}{RMS(x)+\epsilon}\]
  1. Scald and shift
\[y_i=\gamma \hat{x}_i+\beta\]

평균과 표준편차를 모두 계산하는 LN에 비해 RMS만을 계산하는 RMSNorm은 LN에 거의 근접한 성능을 보이면서도 적은 계산량을 차지한다. RMSNorm은 특히 Llama와 같은 거대 언어 모델의 시대에서 LN의 효율적인 대체재로 사용되고 있다.

Shuffling Batch Normalization

Shuffling BN은 일반적인 BN의 대조 학습(contrastive learning) 환경에서의 문제점을 지적한다. 대조 학습에서는 positive pair과 negative pair가 미니배치 내에 혼재되어있는데, 이 때 배치 사이즈가 크면 클수록(즉, negative pair가 많을수록) 성능 향상을 일으킨다.

그러나 미니배치 내의 샘플들간의 공통된 평균/표준편차를 계산하는 BN 과정에서 모델이 일종의 “shared information”을 학습할 수 있고, 이는 모델의 일반화 능력을 저해시킬 수 있다. 따라서 Shuffling BN은 멀티 GPU 환경에서 각 GPU에 적재되는 미니배치간의 feature들을 섞어주어 이러한 문제를 방지하고자 하였다.

자세한 내용은 별도의 포스트에서 다루겠습니다.