4 min to read

QLoRA: 양자화 / 경량화 과정 이해하기

4-bit NormalFloat Quantization, Double Quantization and Paged Optimizers

Quantization

일반적으로 딥러닝에서 가중치 값들은 아래와 같은 부동소수점 형식으로 저장된다. 부동소수점 표현은 부호 비트와 지수부, 가수부로 나뉜다. 부호 비트는 1비트로 고정이며, 전체 비트수가 32개인지, 16개인지, 그리고 지수부와 가수부가 그 중 각각 몇 비트를 차지하느냐에 따라 FP32 / FP16 / BF16 등으로 나뉜다.

양자와(Quantization) 과정은 위와 같은 부동소수점 표현을 더 적은 비트 수로 이산화하는 과정을 의미한다. 더 적은 비트 수를 사용하기 때문에 더 적은 메모리 사용량을 필요로 하고, 현대의 거대 언어 모델을 경량화하는 데 있어 필수적이다.

QLoRA는 현대의 거대 언어 모델을 single GPU에서도 가용할 만한 크기로 양자화하는 기법들을 제시한다.

Background: Block-wise k-bit Quantization

일반적으로 사용되는 양자화 기법에 대해 먼저 살펴보자. FP32 -> Int8로의 양자화를 가정할 때, 그 과정은 아래 수식과 같다. Int8의 경우 표현할 수 있는 숫자의 범위는 $[-127, 127]$로, 부호 비트(1비트)를 제외한 0~127의 $2^7$ 종류의 숫자를 나타낼 수 있다.

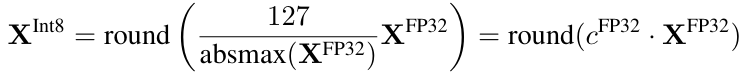여기서 $c^{\text{FP32}}=\frac{127}{\text{absmax(}X^{\text{FP32}})}$는 양자화 상(quantization constant)라고 불리는데, 중요하니 기억해두자.

Int8로 양자화된 값을 FP32로 복원하고자 한다면 아래와 같은 dequantization 과정을 거친다:

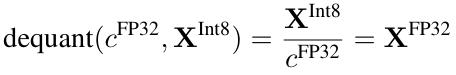
수식만 봐서는 직관적이지 않으니 그림을 통해 살펴보자. 여기 FP32 타입의 10차원 벡터 $X^{FP32}$가 있다.

  1. $X^{FP32}$의 절대값 중 최대값을 찾는다. 아래 예제의 경우 $2.045$.
  2. 전체 값을 최대절대값으로 나눠주면 $[-1, 1]$ 범위의 값들로 scaling된다.
  3. scaling된 값들에 Int8이 표현할 수 있는 최대 숫자인 127을 곱해준 뒤, 소수점 뒤에는 버려준다.

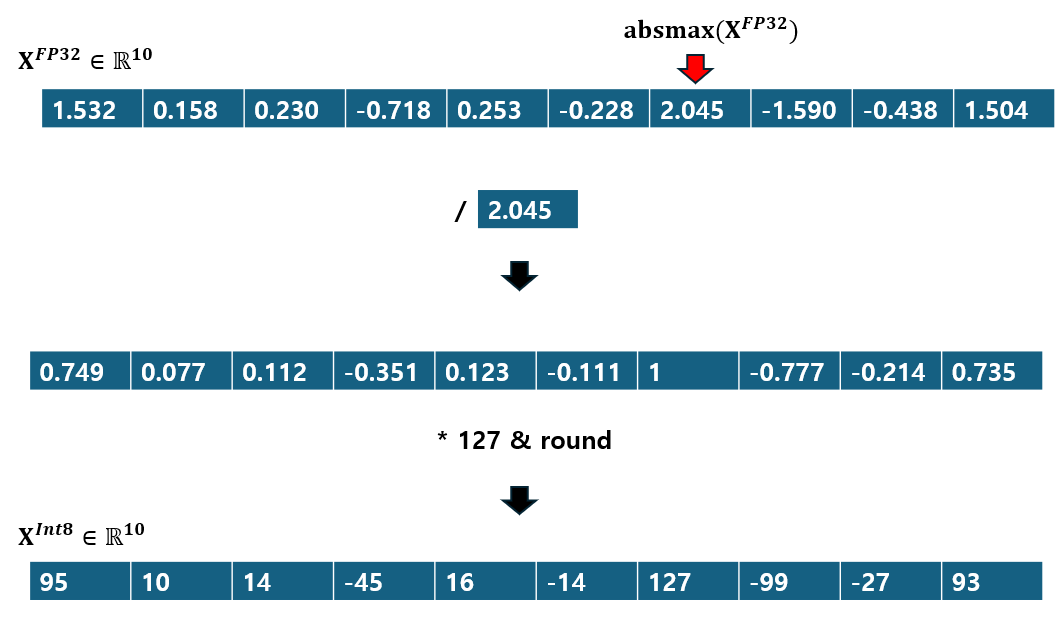
위와 같은 과정으로 FP32 -> Int8 양자화가 이루어진다.

그러나 이런 방법에는 치명적인 문제가 있다. absmax를 사용하기에 만약 벡터 내에 비정상적으로 큰 값(i.e. 이상치)가 포함되어 있을 경우 양자화 구간이 균등하게 나뉘지 못하는 문제가 발생한다.

이게 무슨 말인지 예를 들어 보겠다. 만약 위 예제에서 $X^{FP32}$에 $20$이라는 비정상적으로 큰 값이 포함되어 있었다고 가정해보자.

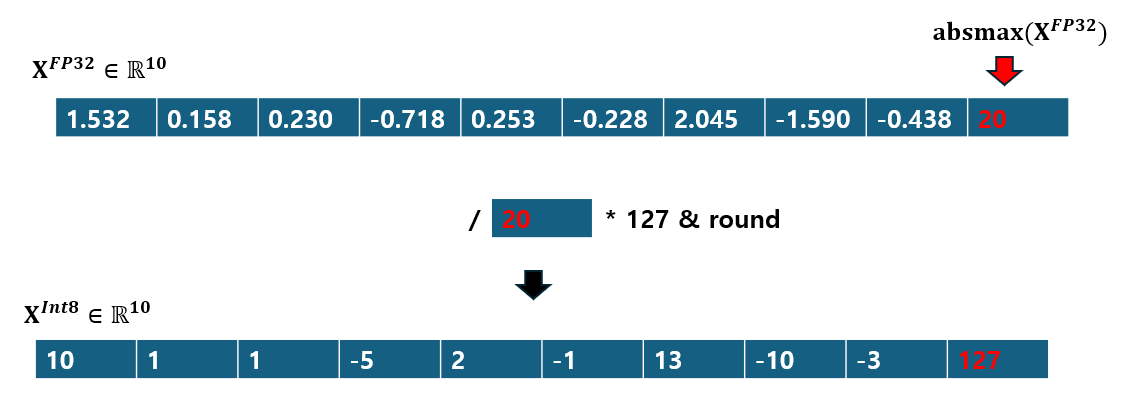
양자화된 결과에서 대부분의 값들은 -10~10 정도의 비교적 작은 값들로 양자화된 반면, 이상치(fp32에서 20)만 혼자 큰 값(int8에서 127)을 가지고 있다. 이 경우 이상치가 아닌 나머지 대부분의 값들은 정밀한 표현이 불가능하다.

이런 문제를 완화하기 위해 일반적으로 전체 벡터를 몇개의 블록들로 나누어, 각각의 블록에 대해 양자화하는 방법을 취하기도 한다.

4-bit NormalFloat Quantization

QLoRA에서는 딥러닝 모델의 가중치를 적은 정보 손실을 감수하며 적은 비트수(i.e. 4비트)로 양자화한 새로운 데이터 타입, NormalFloat (NF)를 새롭게 제안하였다. NF는 Quantile Quantization (QQ)라는 데이터 타입에 근간을 두고 있다.

QQ는 양자화할 때, 가능한 모든 양자화 구간에서 똑같은 개수의 값들이 포함되도록 강제하는 정보이론적으로 최적화된 데이터 타입이다. 벡터(혹은 텐서)의 CDF를 구해서 동일한 개수가 들어가도록 양자화 구간을 나누는 방법인데, 중요한 점은 이 QQ의 optimal한 양자화 구간을 구하는 비용이 꽤 크다는 것이다. 따라서 이를 근사한 알고리즘을 사용하기도 하는데, 이 경우 approximation error를 피할 수 없다.

NF는 이러한 error와 cost 사이의 trade-off를 해결하기 위해 제안되었다. NF는 기본적으로 “신경망(NN)의 가중치는 표준 정규 분포를 따른다”(논문의 Appendix F를 참고)라는 사실에서 출발한다 .

FP32의 벡터를 NF4로 양자화하는 과정을 차근차근 살펴보자.

  1. 가장 먼저 해야할 것은 양자화 구간을 구하는 일이다. 양자화 구간을 구해야 FP32의 값들이 각각 어느 구간에 속하는지 판단하고, 해당 구간으로 대치할 수 있다. 신경망 가중치는 정규분포를 따르기에, 우리는 먼저 어떤 가상의 표준 정규 분포로부터 $2^k$개의 구간을 구한다. 정규분포로부터 양자화 구간을 구한다면, 아래와 같이 평균(0) 쪽에 보다 촘촘한 구간이, 가장자리에 느슨한 구간이 만들어질 것이다.

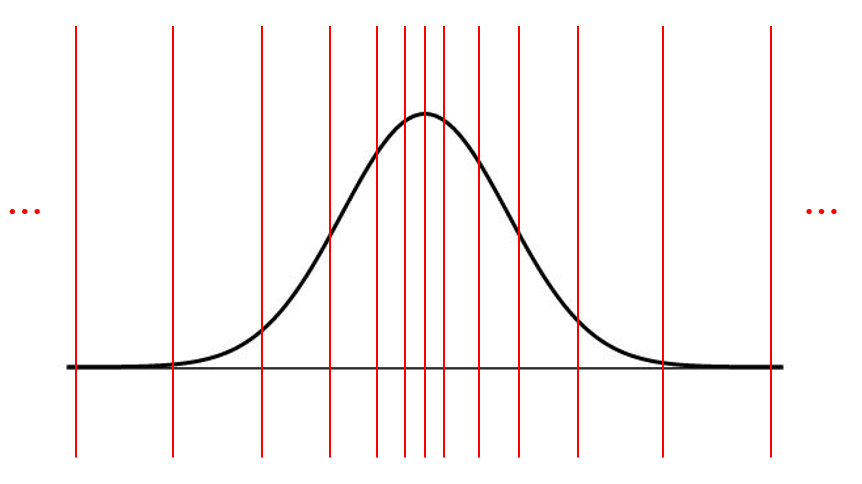그림은 예시이므로 구간 개수나 위치가 정확히 맞지 않을 수 있음.

  1. 위에서 구한 양자화 구간의 경계값들을 $[-1, 1]$ 사이의 범위를 갖도록 scaling한다.

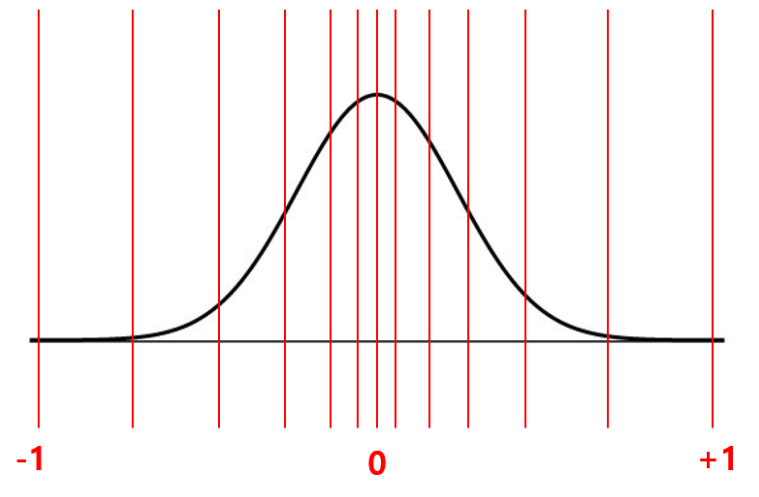
  1. 이제 양자화하고자 하는 대상 벡터(FP32) 값들도 $[-1, 1]$ 사이 범위로 scaling해준다(absmax로 나눠주면 된다). 그러고 나서 위에서 구한 $[-1, 1]$ 범위의 양자화 구간에 맞춰 양자화해준다. 이 때 absmax값(정확히는 quantization constant)은 추후 복원(dequantization) 단계에서 사용할 예정이니 별도로 저장해둔다. 예를 들어, FP32에서 값이 0.238인 값을 양자화한다고 가정하자. 0.238과 가장 가까운 양자화 구간값이 각각 0.2, 0.3이라고 할 때, 0.238의 NF4 양자화된 값은 그 평균인 0.25가 된다.

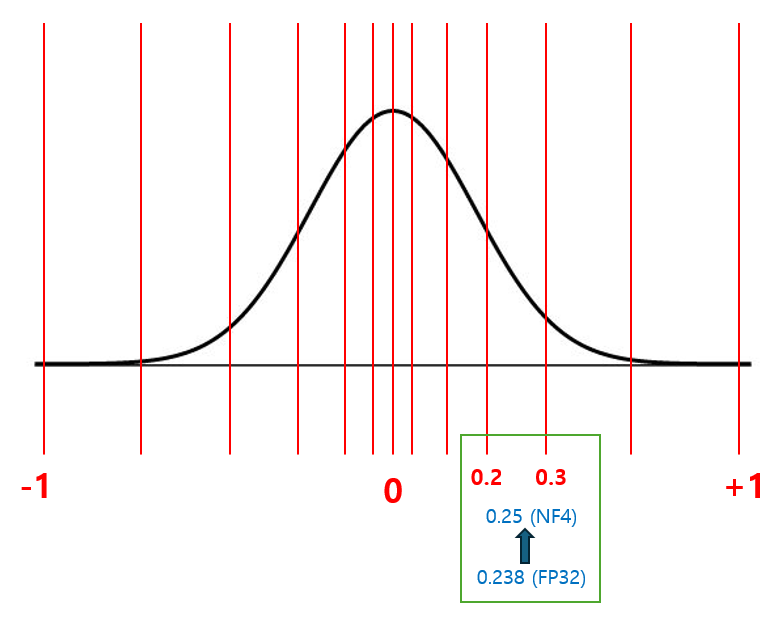
위와 같은 방식으로 정규 분포의 특성을 이용해 적은 정보 손실을 보이는, 균등한 구간(quantile)을 갖는 효과적인 양자화가 가능하다.

양자화된 값을 복원하고 싶다면, 3번 단계에서 저장해둔 quantization constant로 간단히나눠주면 된다 (dequant 수식 참조).

Double Quantization

이쯤에서 의문점이 생긴다. 신경망 가중치를 양자화하는건 알겠는데, 이 과정에서 생기는 양자화 상수 (quantization constant) 값도 따로 저장해줘야 하는것 아닌가? 전체 메모리 사용량은 줄어들었을지 모르겠지만 어쨌든 결국 양자화 상수 저장을 위한 추가적인 메모리 사용량이 필요하기 마련이다.

가령, FP32로 표현된 양자화 상수에 대해 크기가 64인 블록 단위로 양자화한다면, 각 가중치 벡터(텐서)의 각 값마다 32/64=0.5비트의 추가적인 메모리 사용이 더해진다.

NF4에서는 이에 대해 Double Quantization이라는 기법을 도입하여 문제를 해결한다. 신경망 가중치만 양자화하는 것이 아니라, 양자화 상수(quantization constant)까지 양자화하여 저장하여 메모라 사용량을 더욱 절감하겠다는 것이다. 이 경우 FP32의 양자화 상수를 FP8로 양자화한다.

Paged Optimizer

페이징(Paging) 기법은 메모리 사용량이 너무많을 때 일부 사용하지 않는 메모리를 저장 장치(하드디스크 등)에 저장해두었다가 사용할 때 불러오는 방법이다.

Paged Optimizer는 GPU 메모리 사용량이 너무 많아 out-of-memory가 발생하기 전에, GPU에 있던 optimizer state를 잠시 CPU RAM에 페이징해두는 방식이다. 이 때 NVIDIA의 unified memory 기능을 사용하여 CPU와 GPU간의 자동적인 page-to-page transfer를 구현한다고 한다.

QLoRA

마지막으로 QLoRA의 최종 수식을 살펴보며 마무리 맺겠다. QLoRA는 BF16의 가중치를 NF4로 양자화하고, LoRA를 적용한다. LoRA의 수식과 비교하며 이해하면 더 좋다. 구성 요소를 하나씩 살펴보자.

여기서 $X^{BF16}$은 QLoRA의 입력, $Y^{BF16}$는 출력에 해당한다.

먼저 뒤쪽 항의 경우 LoRA Adapter에 해당한다 ($L_1^{BF16},L_2^{BF16}$는 trainable matrices). LoRA Adapter는 NF4로 양자화하지 않고 BF16 (mixed precision) 그대로 사용된다. LoRA Adapter까지 양자화할 경우 성능 저하가 일어날 수 있다.

앞쪽 항의 경우 NF4로 양자화된 가중치 $W^{NF4}$를 double dequantization을 통해 BF16으로 복원하는 부분이 포함되어 있다.

Double dequantization에서는 NF4로 양자화된 신경망 가중치를 BF16로 복원하고, FP8로 양자화된 양자화 상수는 FP32로 복원한다.